你要分析数据，你是别的专业跨过来到心理学方向的；你是本科生，你上课的时候听不懂老师在台上讲些什么鬼；你是个蛇精病，放着周末不在床上多睡几个小时，没事就爱在网上看论文但是又看不懂这些论文里面的统计方法。于是乎你开始在网上搜各式各样的统计科普，恰巧人希咕狗把我的文章权重提上的挺高（或许不会发生），于是乎你就点进来了。

如果这就是发生在你身上的故事的话，那么我们很有缘分，希望这篇文章不会让你感到失望。

PS：因为接了周末远程实习，所以没能达成一周双更……今天写文章的时间也是昨天爆肝写了一天小程序一整天，把今天的工作量一口气做完了才挤出来的时间 QwQ~

问题、假设、实验、结论

我们先从一个最简单的概念讲起，比如有一天王二麻和金三胖对这个问题起了争执：「「程序员」就近胖子多还是瘦子多」。王二麻觉得「程序员」这种奇异的生物应当都是胖子，因为每天就窝在工位前，顿顿外卖，也不运动，久而久之肯定都变成了肥宅；而金三胖则认为包括「程序员」在内的大多数社畜不光没有女朋友，而且精神压力大，每天爆肝，肯定吃不好饭睡不好觉久而久之就都变成了瘦子。

我们先抛开王二麻和金三胖对「程序员」这类生物的误解不谈，就只看这个问题：他们二人所遇到的这个问题不仅是一个科学问题，同时还是一个典型的人口统计学问题。王二麻和金三胖的这段争论的核心是一个「问题」——任何科学研究的开端。而「「程序员」胖子多」、「「程序员」瘦子多」则是一个假设。

王金二人的这段争论已经非常粗糙的完成了典型科学研究四个重要步骤当中的两个。我们在进行科学研究的时候通常都要经历这样四个步骤：「提出问题」、「作出假设」、「进行实验」、「得出结论」。

样本、样本量与总体

王二麻和金三胖大吵三天三夜也没有结果，于是二人便决定找些「程序员」问问体重，来验证自己的想法，这时二人进入了「进行实验」这一环节。

威猛的王二麻选择在每天早上上班时段前往帝都不同的地铁站和公交站，一个个的问等车的人「请问您从事与编程相关的工作吗？」、「您是否方便透露自己的体重」？有点懒的金三胖则在下班之后挑了家楼下的森林公园去做相同的事情。

这时王二麻和金三胖在做的事情被称为：「从总体中抽取样本（抽样）」。

让我们来尝试把这个问题抽象得更加简单一些：在你面前有一大盆各种颜色的糖豆，你想知道哪种颜色的糖豆更多，哪种颜色的糖豆更少。如果想要又快又准的回答这个问题你会怎么做？最快的做法并不是一个一个数糖豆的数量，而是先把这盆豆子摇匀，然后挖出一大勺数一数哪种糖豆更多。

对！你必须把这些糖豆摇匀，这样我们挖出一勺的糖豆才能更好的代表整盆糖豆！

左面的糖豆摇匀了，右面的糖豆没有摇匀，红色代表我们的「勺子」。虽然蓝色和黄色糖豆的数量是一样的，但是从左面挖出的一勺和从右面挖出的一勺，对于总体的代表性是不一样的。

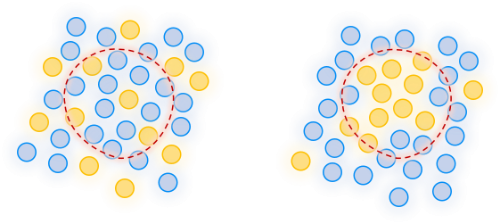
在这个例子中，一盆糖豆就是总体，它包含了我们要研究的所有总体；一勺糖豆就是样本，我们希望这一勺糖豆的颜色比例能够在最大程度上反应整盆糖豆的颜色比例；从盆子里面挖出一勺糖豆的动作就是「抽样」，先摇匀再抽样或者不摇匀就直接抽都是一种抽样方法，但是不同的抽样方法对于总体的代表能力是不一样的，这就是为什么抽样方法可以作为一个单独的技术被人们不断的研究。

让我们带着「样本、总体和抽样」的观点重新来看王二麻和金三胖在做的事情，如果用一种文邹邹的方式来复述一遍他们争论的焦点，这句话可以被翻译为：「相较于一般个体而言，「程序员」的身材究竟是更加臃肿还是更加苗条」？

实际上这句话有很多可以杠的东西，比如：

• 哪里来的「程序员」？北京的？还是上海的？还是灯塔国的？亦或者是火星的（如果有的话）？
• 年龄多大的「程序员」？20 多岁还是 30 多岁还是 60 多岁？
• 做什么的「程序员」？写 C 的？写 C++ 的？ 还是写 C++++ 的？还是 Markdown 「程序员」？
• 什么样的个体算是一般个体？幼儿园的小朋友算吗？隔壁王大爷养的鹦鹉算吗？仲夏夜的好兄弟算吗？还是 Average Joe？

很明显王二麻的调查方法要比金三胖更能代表「程序员」群体，在森林公园抽样的金三胖只能抽到那些「按时加班、生活休闲、说不定还有每天跑步习惯、发亮充裕」的「程序员」，但是我们都知道，相当多「程序员」还是在享受福报，无暇生活的。

不过这两个人的调查方法能够反应整个中国的「程序员」群体的体重情况吗？能够反应全世界「程序员」的体重情况吗？这个问题当作课后作业留给各位读者思考好了 σ`∀´)σ

统计指标与统计量

统计指标

这时金三胖想起了自己的两个「程序员」朋友，两个人虽然体重差不多，但一个身材矮且壮实，另外一个则是又高又瘦的火柴棍。虽然体重一样但是一个很瘦另外一个不瘦。所以用体重这个指标当作判断一个人胖瘦显然是不合适的。除此以外不同年龄的人体态本身就会发生自然变化，所以金三胖提议两个人重新收集数据，这次要额外收集「程序员」们的身高和年龄，再用 BMI 的公式来算一算一个人是胖还是瘦。

从这件事情上我们可以看到，为了探究一件事情的本质，我们可以选择很多种统计指标。比如探究一个人是胖还是瘦，我们可以单纯的收集一下体重，但是这往往不能反映事实，同时考虑了身高的 BMI 可能是一个更好的指标。那么我们不妨多想一步，只有身高和体重两个指标就能反应一个人是胖还是瘦吗？事实上并不能，脂肪要比肌肉的密度低很多，同样身高体重的两个人，一个人很可能是松软的沙发土豆，而另外一个是肌♂肉♂兄♂贵。如果我们再加入一个体脂比作为衡量一个人身材的指标，或许就科学很多。不过我们几乎没有办法在早高峰的帝都地铁站拿着体脂仪一个个给人侧量体脂，所以这件事情姑且放下，对于这个话题感兴趣的读者可以参考一下这篇台湾的《体能常模报告书》，里面有更细致的探讨。

抽样分布与假设检验

王二麻和金三胖姑且算是拿到了一个能够在某种程度上反应「程序员」是胖还是瘦的客观指标，那么接下来我们要怎么样判断「程序员」群究竟是胖还是瘦呢？假设帝都全体人口的 BMI 均值为 22.58，那么「程序员」群体的体重究竟比这个数值高还是低呢？高多少才算高呢？高 0.01 算高么？高 0.1 算么？高 1 呢？高 10 呢？

「高多少才算高」是一个非常好的问题。但是为了解决这个问题我们需要一些预备知识。

抽样分布

回到糖豆的例子，除非每次我们每次都把一盆糖豆都数一遍（即样本量等于总体），否则每次抽样得出来的不同颜色比例不太可能会精确的等于全体糖豆颜色的比例，这就是我们在进行统计时没办法忽视的误差。

在糖豆被摇匀的前提下，同样的一盆糖豆，我们在不同的地方挖一勺，所得到的糖豆颜色比例会存在差异，比如左面的图挖出了五颗黄色的糖豆，右面的图却挖出了三颗黄色的糖豆。

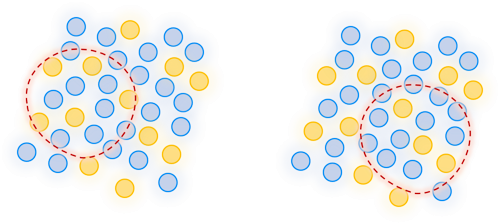
对于全体「程序员」也一样，随机找到一百人，算一下平均 BMI，再随机抽出一百人，算一下平均 BMI，大概率得出的数字不是一致的。但是这些不一致的平均 BMI 都能在一定程度上接近全体「程序员」的平均 BMI 指标，进而反应全体「程序员」的胖瘦。

那么接下来让我们来做一件比较疯狂的事情，如果我们从全体「程序员」这个大池子中，有放回的抽一百个人，算一下 BMI 的均值，再把这些人丢回池子里，再抽一百人，再算一下均值。将这件事情重复十万次，那么会发生什么呢？

答案是，这些均值会形成一个正态分布。

这件事情其实比较符合直觉，平均数是一个无偏的统计量（究竟什么是无偏我会在后面的文章再讲），这意味着在抽样方法得当的情况下，抽样的均值应当能够准确的反应总体的均值。那么进行大量抽样时，抽出来的样本均值一定接近总体均值的多，和总体均值差很多的少。

这时我们可以得出这样的一个结论：通常来讲，如果我们从一个总体中有放回的随机抽取数量足够的样本（通常必须大于 30），且次数足够多，并计算每个样本的平均数。那么这些平均数会形成一个正态分布，正态分布的中心为总体的均值。这件事情有个很高端的名字叫做中心极限定理，翻译成人话就是「从总体上做一次样本量不小于 30 的抽样，得到的样本均值接近总体均值的概率大，偏离总体均值的概率小」。

考虑到有些朋友可能不信，所以我们在这里做一个非常迷你的统计学实验：

• 建立若干个遵循不同分布的总体；
• 从总体中抽样十万次，并计算每次抽出样本的平均数（有放回抽样）；
• 绘制不同样本量下的平均值分布。

不同总体分布的平均数的抽样分布。

上面这张图的第一行展示的就是不同的总体分布，从第二行开始展示的就是不同样本量下的抽样分布，每一列是一种分布，每一行对应的是不同样本量的大小。比如第二列第三行描绘的是：「总体为多峰分布，样本量为3，抽样十万次时得到的抽样分布」。对于第一行，横轴代表的是个体的的具体统计指标（比如 BMI、身高、体重），纵轴表达的是这个值包含的个体数究竟是多还是少，换到 BMI 的例子里面来讲，全中国所有的「程序员」的分布。从第二行开始，就是抽样分布，横轴不再代表具体的统计指标而代表着统计指标的均值（比如一百个「程序员」的平均 BMI），纵轴表示究竟有多少个样本的均值是这个数。

第一行的各个分布就是总体分布，从第二行开始的所有分布就是抽样分布。

从这张图中我们可以非常明确的看出如果总体的分布是对称的，那么随着样本量的增加，抽样分布会很快的收敛于正态分布。

除了这点之外，我们不难注意到，随着样本量的增加，抽样分布会变得越来越窄，这一点体现在横轴上，随着行数的增加，每一行横轴的数字范围开始变得越来越小。因为样本量越大，样本就越能代表总体，对样本进行抽样，其均值接近总体均值的概率也就会变得越大。一个比较极端的例子是，如果我们一口气测量了全中国所有「程序员」的体重，那么无论重复这个过程多少次，得到的均值永远都会是全中国「程序员」的均值，因为样本量等于总体量。但是如果我们每次只抽十个人的话，均值的不确定性就会增强，反映到分布上就是分布变宽，你可以得到各种各样的数字，而非「全中国「程序员」的均值」这个单一的数值。

除此以外抽样分布的形态还与总体的方差有关：

不同均值与方差分布的平均数的抽样分布，不同颜色代表不同的分布，色彩标识后面的信息包含了均值与方差，均值在括号外，方差在括号内。

上面这张图绘制了不同方差、均值的正态分布，他们的抽样分布是什么样的。从这张图中我们可以发现，总体的方差如果变大，抽样的分布的宽度也会变大。

接下来让我们来总结一下平均数抽样分布的性质：

• 总体的均值决定了抽样分布的中心；
• 随着样本量的增加，均值的抽样分布总是会收敛于正态分布；
• 样本量越大，抽样分布就越狭窄，样本量越小，抽样分布就越宽；
• 总体的方差也与抽样分布的宽窄有关，总体方差越大，抽样分布越宽。

一些比较「数学」的知识

平均数的抽样分布是一个正态分布，决定正态分布形态的参数有两个，均值和标准差（关于正态分布的基本知识可以读这篇，如果还记得初中老师怎么教的话，不看也成）。

我们刚刚讲到，正态分布的均值就是总体的均值，那么正态分布的方差是什么呢？我们前面讲到它由总体的方差和抽样的样本量决定，其具体的公式是这样的：

$$SE=\frac{s}{\sqrt{n}}$$

这个值又叫标准误。

如果我们将纵轴从「均值出现的次数」改成「均值出现的概率」，我们就得到了「概率密度函数」。值得注意的一点是，累积分布函数的曲线下面积永远是 $1$。

扩展阅读

我们知道如果想知道一批数据最基本的样子，可用的描述统计量不仅有平均数，还有：

• 集中量数：中位数、众数、几何平均数、调和平均数
• 差异量数：全距、四分位差、平均差、方差和标准差

我花了一天的时间把方差、全距、中位数和几何平均数的抽样分布跑了一遍，如果你对这些统计量的统计分布感兴趣的话可以点链接进去看看，源代码在这里，如果你想要自己造个统计量或者试试其他统计量的抽样分布，可以在这份代码的基础上做一些修改重新跑一跑。

假设检验

王二麻和金三胖通过各问了 20 名「程序员」，得到的「程序员」平均体重分别是 22.91 和 22.03，而帝都人口的平均 BMI 是 22.58。这时两个人吵起来了，因为他们手里的数据都支持了自己的想法。

但事实上是这样吗？王二麻的数据显示帝都「程序员」比帝都人的 BMI 平均高了 0.33，金三胖的数据则认为帝都「程序员」比帝都人的 BMI 平均少了 0.55，事实上都没有多很多。

这就引出了另一个问题：「多多少算多」。多 0.05 算多吗？多 0.1 算多吗？多 1 算多吗？多 10 算多吗？

抽样分布可以在一定程度上解决我们的问题。根据前面的讨论我们会发现，对特定的一个总体进行抽样并计算均值，这个均值接近总体均值的概率大，偏离总体的概率小。那么只要知道了总体的分布形态，就可以知道进行一次抽样，抽得样本均值为特定值的概率。

下面让我们来实际的利用先验分布来尝试解决一个问题。

假设一份人口普查报告称帝都全体人口的 BMI 均值为 22.58，方差为 2.41（事实上基本不会有什么普查报告跟你讲这些东西），那么我们就可以画出总体分布的概率密度函数，均值是 22.58，方差是标准误 $\frac{2.41}{\sqrt{20}}=0.539$。

帝都全体人口 BMI 的分布，黑色的虚线分别表示王二麻和金三胖的样本均值：2.91 和 22.03，红色的实线表示帝都人口的平均 BMI。

接下来，我们将问题转化为：如果我们从全帝的人口中完全随机的抽取一个容量为 20 的样本，那么得到均值大于 22.91 或均值小于 22.03 的样本的概率有多大？

我们可以通过概率密度函数曲线下的面积来求得这个概率。比如，如果我们想要求均值大于 22.91 的概率，只需要计算下图蓝色区域的面积，而想要知道均值小于 22.03 的概率，仅需要计算绿色区域的面积。

蓝色区域代表均值大于 22.91 的概率，绿色区域代表均值小于 22.03 的概率

通过计算（至于具体是怎么算的，你可以暂时把它当成魔法），我们发现从全帝都人当中随机抽一个样本量为 20 的样本，样本均值小于 22.03 的概率是 15.37%，而样本均值大于 22.91 的概率是 27.01%，换句话说，只要我们随机进行三到六次就有可能得到一个这样的样本，这样的结果一定是不可靠的。一般来讲，只有这个概率小于 5% 我们才认为这个结果可信。

那么我们可以怎样得出更加可信的结果呢？最简单的办法就是增加样本量，让抽样分布变得更加狭长，这样分布两侧的面积就会减小。

样本量的大小影响了抽得特定均值样本的概率。

对了，这个概率就是我们经常说的 $p$ 值。

结语

王二麻和金三胖依旧没能知道「程序员」究竟是胖还是瘦，他们的旅途还将继续。不过我已经写不动了，所以故事暂且讲到这里。

今天这篇文章简要的介绍了实验设计的基本知识、重新阐述了样本与总体，及其统计学意义，同时降到了假设检验系统会用到的基础概念。「样本」和「总体」两个概念是我着笔墨最多的部分，也是本科上课的时候老师完全没有讲明白的部分，个人认为这块的知识对于理解统计非常重要，是最基础的一环。对于想要弄懂基础统计的朋友们还请多花些功夫把这两个概念以及其对应的「总体分布」、「抽样分布」都搞明白。

这一系列文章是按照螺旋向上的顺序设计的，下次将会对假设检验系统做更加详细的介绍，同时也会具体的讲讲$Z$检验、$T$检验、方差分析和线性回归方程。

这一篇文章从构思到行文作图花了三天才整完，简直累死我了，保守估计要把这个故事讲完至少也得四篇文章真是给自己挖了个大坑。下次什么时候更看缘分吧……咕咕咕~

本篇文章是遗迹计划的一部分，文章内容谢绝转载，转载图片请依照 CC-BY 4.0 协议。

以上，就是本文的全部内容，莉莉爱你 ヽ(✿ﾟ▽ﾟ)ノ♥~